Repressors & Leaks

Theoretically, a single gene could keep producing a single protein indefinitely, if it had the energy. From a circuit design perspective, though, that’s not very interesting. In order to do something more interesting, we need some way to regulate production.

Repressors enable gene regulation. They bind to specific binding sites at or near the promoter of a gene (remember, that’s where transcription starts) and inhibit transcription initiation. An example of this in bacteria is the Lacl repressor in E. coli. Normally, it inhibits the gene for lactase production. When lactose is present, though, a modified form of lactose (allolactose) binds to Lacl, and prevents it from inhibiting lactase production. Lactase is then produced, and the lactose is digested. Lacl is then free to bind to the gene again, inhibiting lactase production until the next time lactose appears.

Here’s a diagram, with the repressor labeled R:

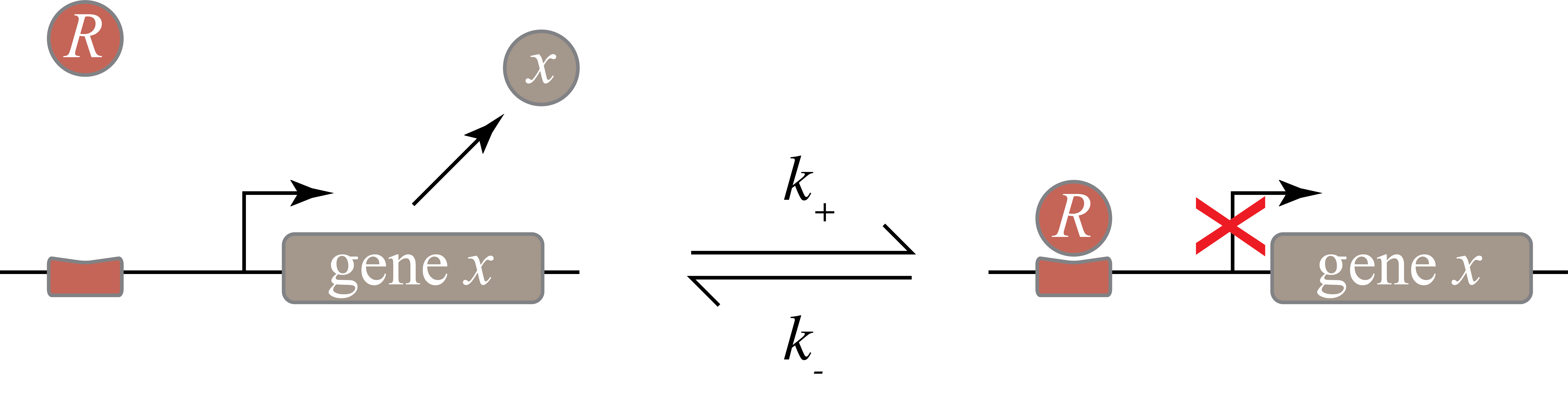A diagram of a gene with and without a repressor. Credit: CalTech

Binding and unbinding a repressor can be modeled through this chemical equation:

$$\ce{P + R <=>[k_+][k_-] P_\mathrm{bound}}$$

We can model the dynamics of this reaction using mass action kinetics: essentially, the rate of a reaction is proportional to the product of the concentrations of its products. Within a single cell, an individual site is either bound or unbound. Averaged over a population of cells, though, we can talk about the mean occupancy of a site. If \(r\) is the concentration of repressor, \(p\) is the concentration of unbound promoter, and \(p_\text{bound}\) is the concentration of bound promoter, we can say that:

$$\frac{dp}{dt}=-k_+pr+k_-p_\text{bound}$$

For this situation, we can assume a separation of timescales, because the rate at which the repressor binds to and unbinds from the DNA is generally very fast compared to the rates at which mRNA and protein concentrations vary. This is generally a reasonable assumption in bacteria, but be aware that in some situations, as in some genes in mammals, it might not work. Here, though, we can handily assume that the binding and unbinding is happening quickly enough that \(\frac{dp}{dt}\approx0\). To find the concentrations, then, we can set the above equal to zero and solve for whatever we want.

Specifically, if \(p_\text{tot}\) is the total concentration of promoters, both bound and unbound, then we can set \(p_\text{bound}=p_\text{tot}-p\) and rearrange the equation to give the fraction of free promoters:

$$\frac{p}{p_\text{tot}}=\frac1{(1+r/K_d)}$$

Where \(K_d\) is the dissociation constant — a measurement of the likelyhood that a repressor will unbind from its binding site — calculated as \(\frac{k_-}{k_+}\). Because we have a separation of timescales and can simplify things, the rate of production of gene product should be proportional to the probability of the promoter being unbound:

$$\beta(r)=\beta_0\frac{p}{p_\text{tot}}=\frac{\beta_0}{1 + r/K_d}$$

This is the simple binding curve. We’ll be using and building on it over the course of the next few sections. It has three parameters:

  • \(K_d\) is the concentration of repressor at which the production is reduced to half its maximum value.
  • \(\beta_0\) is the maximum expression level, acting as a coefficient for the rest of the function.
  • \(r\) is the concentration of repressor.

For small values of \(r\), note that the slope is \(-\frac{\beta_0}{K_d}\). Here’s a graph to play around with (the line represents the initial slope):

Leaky expression

Unfortunately, repressors aren’t perfect. Many genes can never be entirely repressed, and have a baseline, or “basal”, level or expression. We can represent this by adding another term, $\alpha_0$, to $\beta(r)$:

$$\beta(r)=\frac{\beta_0}{1 + r/K_d}+\alpha_0$$

Why does this happen, you ask? There are a couple of reasons:

  1. Molecular interactions inside a cell are always probabilistic, and repressors are constantly binding and unbinding.
  2. Even if there are more repressors than genes to repress, there is typically a small, but finite, amount of time between the unbinding and re-binding of a repressor. During this time, transcription initiation can still happen. Remember: repressors only bind to the promoter, so once transcription is initiated, protein synthesis can still happen, even if a repressor binds during the process.

Because leaks are so common, it’s important to make sure that important parts of your circuits don’t depend on the complete absence of leaky expression.

Onwards!